平均値: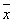
変量を全て足し合わせ、資料の個数で割った値を平均値といい、![]() (「
(「 ![]() バー」と読む)で表します。
バー」と読む)で表します。
![]()
[例] 10, 20, 30, 40, 50 の平均値
![]()
中央値(メジアン):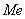
変量を小さい順に並べたとき、中央にある変量の値を中央値(メジアン)といいます。資料の個数が奇数個の場合は中央にある変量の値を中央値とすればよいのですが、偶数個の場合は中央にある2つの変量の値の平均値を中央値とします。
[例]
(1) 10, 20, 30, 40, 50 の中央値
![]()
(2) 10, 20, 30, 40, 50, 60 の中央値
![]()
大事なことなので繰り返します。資料の個数が偶数個の場合は中央にある2つの変量の値の平均値を中央値とします。
最頻値(モード):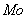
度数が最も多く現れる変量の値を最頻値(モード)といいます。
[例] 10, 20, 20, 30, 30, 30 の最頻値
![]()
[例題]
|
階級 |
度数 |
|
31〜40 |
2 |
|
41〜50 |
2 |
|
51〜60 |
6 |
|
61〜70 |
4 |
|
71〜80 |
4 |
|
81〜90 |
2 |
次の表は、あるクラス20人に対して実施した数学の試験の得点をまとめたものである。
(1) 平均値を求めよ。
(2) 中央値(メジアン)を求めよ。
(3) 最頻値(モード)を求めよ。
[解答]
|
階級 |
階級値
|
度数
|
|
|
31〜40 |
35.5 |
2 |
71 |
|
41〜50 |
45.5 |
2 |
91 |
|
51〜60 |
55.5 |
6 |
333 |
|
61〜70 |
65.5 |
4 |
262 |
|
71〜80 |
75.5 |
4 |
302 |
|
81〜90 |
85.5 |
2 |
171 |
|
|
|
合計 |
1230 |
|
|
|
平均 |
61.5 |
(1) 61.5
(2) 60.5
(3) 55.5
[解説]
資料が表で与えられた場合、表に変量は記されていないので、変量の変わりに階級値を用いて平均値、中央値、最頻値を求めることになります。階級値とは各階級の中央の値のことでしたので、それを踏まえて表を整理すると右のようになります。
(1) 平均値
![]()
(2) 中央値(メジアン)
20人(偶数)のクラスなので、点数が低いほうから数えて10人目と11人目の属する階級それぞれの階級値の平均値を取ります。10人目は51〜60の階級に、11人目は61〜71の階級に属していますので、それぞれの階級値55.5と65.5の平均値が中央値(メジアン)となります。
![]()
しつこいようですが、大事なことなので最後にもう一度だけ繰り返します。資料(この問題では階級値)の個数が偶数個の場合は中央にある2つの変量の値の平均値を中央値とします。
(3) 最頻値(モード)
最も度数が多いのは51〜60の階級です。よって、その階級値55.5が最頻値となります。
仮平均: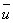
例えば、5人の生徒A〜Eのテストの得点がそれぞれ 72, 85, 63, 54, 66 であるとします。このとき、得点の平均値は
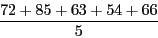
で計算できますが、この足し算はあまりしたくありません。とはいっても、まだこのくらいなら計算する気がしますが、これが10人の生徒A〜Jの得点 72, 85, 63, 54, 66, 70, 87, 66, 52, 65 だったらどうでしょうか?
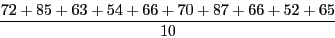
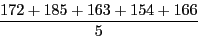
計算したくないと思います。
このように、データの数が多かったり、変量の値(や階級値)が大きくて計算するのが大変な場合、それぞれの変量の値(や階級値)から適当な数(仮平均)を引いた値を用いると、計算を楽にすることができます。
後者 (172, 185, 163, 154, 166) の平均値を計算する場合、全てのデータの百の位の値が1であることに注目し、それらは無視して十の位と一の位だけを計算した後に、百の位の1を付け加えると思います。この工夫はほとんど意識せずに行われますが、みなさんは仮平均の考え方を利用しているのです。前者 (72, 85, 63, 54, 66, 70, 87, 66, 52, 65) の平均値を計算する際にも、これと似た工夫をすることにより、計算を楽にすることができます。
この場合 (72, 85, 63, 54, 66, 70, 87, 66, 52, 65) は、ざっと見たところ平均値が70くらいになりそうなので、まずは全ての数から70(これを仮平均と言います)を引いた値を計算します。すると、+2, +15, -7, -16, -4, 0, +17, -4, -18, -5 となります。次に、これらの平均値を求めます。
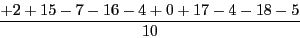
すると、-2になるので、これに仮平均 70 を足します。このようにして求まった値 68 は、普通に計算して求めた値 68と確かに一致します。
※ここから先の話は抽象的で難しいかもしれないので、理解できない場合は読み飛ばしてしまっても構いません。
それぞれの階級値(や変量の値)![]() から
から![]() を引いた
を引いた![]() (
(![]() )を用いて計算した仮平均
)を用いて計算した仮平均![]() と平均値
と平均値![]() の間には
の間には
![]()
という関係が成り立ちます。みんな平等に![]() ずつ引いたのですから、
ずつ引いたのですから、![]() となるのを理解するのは難しくないと思います。そして、これを式変形すると上の式が導かれます。
となるのを理解するのは難しくないと思います。そして、これを式変形すると上の式が導かれます。
|
階級 |
階級値
|
|
度数
|
|
|
31〜40 |
35.5 |
-20 |
2 |
-40 |
|
41〜50 |
45.5 |
-10 |
2 |
-20 |
|
51〜60 |
55.5 |
0 |
6 |
0 |
|
61〜70 |
65.5 |
10 |
4 |
40 |
|
71〜80 |
75.5 |
20 |
4 |
80 |
|
81〜90 |
85.5 |
30 |
2 |
60 |
|
|
|
|
合計 |
120 |
|
|
|
|
仮平均 |
6 |
|
|
|
|
平均 |
61.5 |
では、先ほどの例題で、![]() 、
、![]() とおいて仮平均を求めてみましょう。
とおいて仮平均を求めてみましょう。
まず、それぞれの階級値に![]() なる変数変換を施します。
なる変数変換を施します。
![]()
![]()
![]()
![]()
![]()
![]()
・
・
・
![]()
![]()
![]()
次に、それを用いて仮平均を求めます。
![]()
![]()
![]()
最後に、![]() とすれば平均値が求まります。
とすれば平均値が求まります。
![]()
これは、先ほど普通に平均値を計算した結果と一致していることが確認できます。
ところで、ここでは![]() とおきましたが、計算が簡単になりそうな値を適当に決めただけですので、実際は55.5でなくてもかまいません。45.5でも、55でも、50でも何でも構いません。ただし、センター試験では問題文で誘導される可能性もありますので、その場合は誘導に従って下さい。
とおきましたが、計算が簡単になりそうな値を適当に決めただけですので、実際は55.5でなくてもかまいません。45.5でも、55でも、50でも何でも構いません。ただし、センター試験では問題文で誘導される可能性もありますので、その場合は誘導に従って下さい。